描述

Given a sorted linked list, delete all duplicates such that each element appear only once.

For example,
Given 1->1->2, return 1->2.
Given 1->1->2->3->3, return 1->2->3.

描述

In a string S of lowercase letters, these letters form consecutive groups of the same character.

For example, a string like S = "abbxxxxzyy" has the groups "a", "bb", "xxxx", "z" and "yy".

Call a group large if it has 3 or more characters. We would like the starting and ending positions of every large group.

The final answer should be in lexicographic order.

Example 1:

1
2
3

Input: "abbxxxxzzy"
Output: [[3,6]]
Explanation: "xxxx" is the single large group with starting  3 and ending positions 6.

Example 2:

1
2
3

Input: "abc"
Output: []
Explanation: We have "a","b" and "c" but no large group.

Example 3:

1
2

Input: "abcdddeeeeaabbbcd"
Output: [[3,5],[6,9],[12,14]]

Note: 1 <= S.length <= 1000

描述

There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, ..., N-1, and each room may have some keys to access the next room.

Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, ..., N-1] where N = rooms.length. A key rooms[i][j] = v opens the room with number v.

Initially, all the rooms start locked (except for room 0).

You can walk back and forth between rooms freely.

Return true if and only if you can enter every room.

Example 1:

1
2
3
4
5
6
7

Input: [[1],[2],[3],[]]
Output: true
Explanation:  
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3.  Since we were able to go to every room, we return true.

Example 2:

1
2
3

Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.

Note:

1. 1 <= rooms.length <= 1000
2. 0 <= rooms[i].length <= 1000
3. The number of keys in all rooms combined is at most 3000.

描述

A rectangle is represented as a list [x1, y1, x2, y2], where (x1, y1) are the coordinates of its bottom-left corner, and (x2, y2) are the coordinates of its top-right corner.

Two rectangles overlap if the area of their intersection is positive. To be clear, two rectangles that only touch at the corner or edges do not overlap.

Given two (axis-aligned) rectangles, return whether they overlap.

Example 1:

1
2

Input: rec1 = [0,0,2,2], rec2 = [1,1,3,3]
Output: true

Example 2:

1
2

Input: rec1 = [0,0,1,1], rec2 = [1,0,2,1]
Output: false

Notes:

1. Both rectangles rec1 and rec2 are lists of 4 integers.
2. All coordinates in rectangles will be between -10^9 and 10^9.

描述

Let’s call an array A a mountain if the following properties hold:

• A.length >= 3
• There exists some 0 < i < A.length - 1 such that A[0] < A[1] < ... A[i-1] < A[i] > A[i+1] > ... > A[A.length - 1]

Given an array that is definitely a mountain, return any i such that A[0] < A[1] < ... A[i-1] < A[i] > A[i+1] > ... > A[A.length - 1].

Example 1:

1
2

Input: [0,1,0]
Output: 1

Example 2:

1
2

Input: [0,2,1,0]
Output: 1

Note:

1. 3 <= A.length <= 10000
2. 0 <= A[i] <= 10^6
3. A is a mountain, as defined above.

描述

Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.

Example 1:

1
2
3

Input: S = "ab#c", T = "ad#c"
Output: true
Explanation: Both S and T become "ac".

Example 2:

1
2
3

Input: S = "ab##", T = "c#d#"
Output: true
Explanation: Both S and T become "".

Example 3:

1
2
3

Input: S = "a##c", T = "#a#c"
Output: true
Explanation: Both S and T become "c".

Example 4:

1
2
3

Input: S = "a#c", T = "b"
Output: false
Explanation: S becomes "c" while T becomes "b".

Note:

1. 1 <= S.length <= 200
2. 1 <= T.length <= 200
3. S and T only contain lowercase letters and '#' characters.

Follow up:

• Can you solve it in O(N) time and O(1) space?

描述

At a lemonade stand, each lemonade costs $5.

Customers are standing in a queue to buy from you, and order one at a time (in the order specified by bills).

Each customer will only buy one lemonade and pay with either a $5, $10, or $20 bill. You must provide the correct change to each customer, so that the net transaction is that the customer pays $5.

Note that you don’t have any change in hand at first.

Return true if and only if you can provide every customer with correct change.

Example 1:

1
2
3
4
5
6
7

Input: [5,5,5,10,20]
Output: true
Explanation: 
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.

Example 2:

1
2

Input: [5,5,10]
Output: true

Example 3:

1
2

Input: [10,10]
Output: false

Example 4:

1
2
3
4
5
6
7

Input: [5,5,10,10,20]
Output: false
Explanation: 
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can't give change of $15 back because we only have two $10 bills.
Since not every customer received correct change, the answer is false.

Note:

• 0 <= bills.length <= 10000
• bills[i] will be either 5, 10, or 20.

描述

Given a balanced parentheses string S, compute the score of the string based on the following rule:

• () has score 1
• AB has score A + B, where A and B are balanced parentheses strings.
• (A) has score 2 * A, where A is a balanced parentheses string.

Example 1:

1
2

Input: "()"
Output: 1

Example 2:

1
2

Input: "(())"
Output: 2

Example 3:

1
2

Input: "()()"
Output: 2

Example 4:

1
2

Input: "(()(()))"
Output: 6

TOREVIEW

描述

Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

Example 1:

1
2
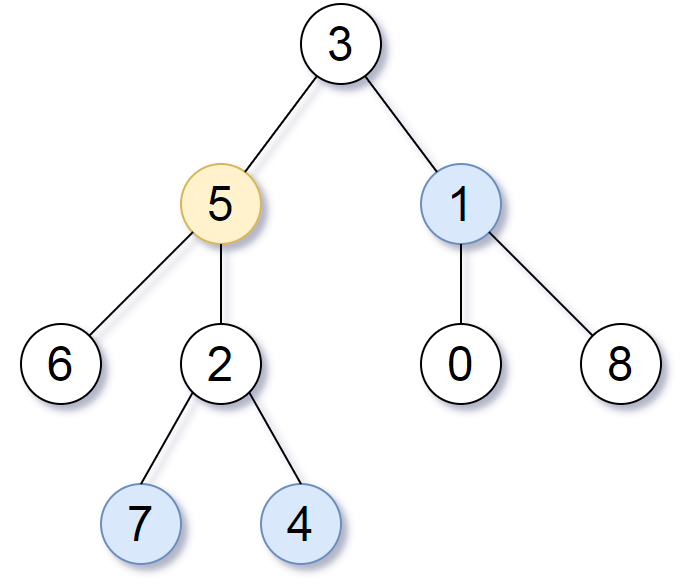
3

Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

Example 2:

1
2

Input: root = [1], target = 1, k = 3
Output: []

Constraints:

• The number of nodes in the tree is in the range [1, 500].
• 0 <= Node.val <= 500
• All the values Node.val are unique.
• target is the value of one of the nodes in the tree.
• 0 <= k <= 1000

描述

Given a matrix A, return the transpose of A.

The transpose of a matrix is the matrix flipped over it’s main diagonal, switching the row and column indices of the matrix.

Example 1:

1
2

Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: [[1,4,7],[2,5,8],[3,6,9]]

Example 2:

1
2

Input: [[1,2,3],[4,5,6]]
Output: [[1,4],[2,5],[3,6]]

Note:

1. 1 <= A.length <= 1000
2. 1 <= A[0].length <= 1000